When it comes to the rounding system, everyone should be familiar with decimal, because most of life uses decimal, and we have learned the four arithmetic of decimal since elementary school. Since humans are so familiar with decimal, why don’t computers use the same decimal as humans?
Binary representation
The bottom layer of the computer is composed of a bunch of electronic circuits. Let’s take a look at the simplest circuit example:
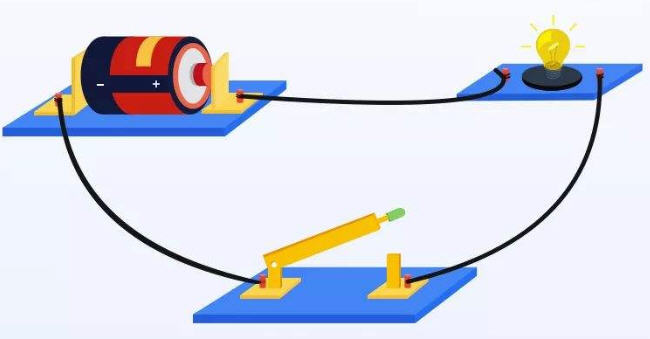
You may have guessed the function of the circuit above:
When the switch is closed, the light bulb is on
When the switch is off, the bulb is off
We can use the closed switch to represent 1, and the open switch to represent 0. This is a simple binary circuit.
Similarly, the magnetic disk is actually composed of many small magnets. The N pole of the magnet indicates 1, and the S pole indicates 0. So each small magnet has two states of 0 and 1 just like a switch.
Early components can only represent these two states (such as on and off, N and S, etc.), which is why computers use binary. Think about it, if the computer uses decimal, this electronic component must have ten states, how complicated it should be!
Binary bits and bytes
However, the number that can be expressed with only one digit is limited. For example, binary is 0-1, decimal is 0-9, and hexadecimal is 0-15. Of course, a single number cannot meet our needs. If a computer can only handle the range of 0-1, humans can only handle the range of 0-9, and a disk can only store the two numbers 0 and 1, then social development may be early. Just stand still!
Smart humans choose to count with more digits, in decimal we can use eight digits to represent numbers within 100 million, the same is true for binary. We generally call the 8-bit binary a byte. One byte can represent 0-255 values (think why 255?). If you want to process more information, you need more bits. For example, a 64-bit CPU can process more and faster information than a 32-bit CPU.
The representation of “3” in binary
Now that you know so much, how do you represent binary 3 in decimal?
In fact, this problem is the same as “9 + 2 in decimal”. That is through carry. Decimal is one for every ten, and binary is one for every two.
Now let’s see how to express 3: in binary:
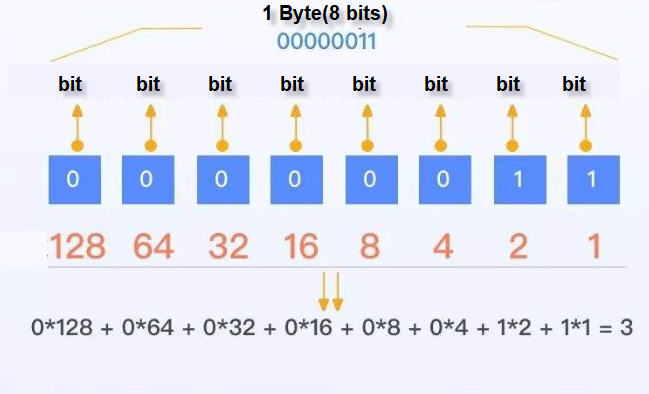
The above picture clearly shows the calculation process in binary, is it the same logic as decimal decimal?
In a byte (8-bit binary number), the weight of each digit is different, namely 1, 2, 4, 8, 16, 32, 64, 128. Similarly, decimal is one, ten, one hundred, one thousand, ten thousand, etc.
Now, do you already understand binary?

there are 10 type of peoples, who understand binary, and who don’t understand binary